| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- matlab
- 선형대수학
- 물리학
- ┌─┐
- css3
- 나무위키
- IT
- Nemeth Braille
- CSS
- 확률
- html
- 프로그래밍
- HTML5.
- C++
- Inkscape
- html5
- LaTeX
- 리브레위키
- javascript
- 자바스크립트
- C언어
- python
- 글이_점점_짧아지고_있습니다.
- Java
- 오늘의 문제
- 프로그래밍 언어
- 수학
- C
- 점자
- 위키
- Today
- Total
SturdyCobble's Study Note
[Python] Buffon's Needle Problem in Polygon version(Buffon's polygon) 본문
[Python] Buffon's Needle Problem in Polygon version(Buffon's polygon)
StudyingCobble 2019. 9. 4. 22:08NOTICE : 독학인 만큼, 잘못된 내용이 있을 수 있습니다. 내용 지적은 언제나 환영합니다.
더 이상 이 블로그에는 글을 올리지는 않을 예정입니다. 그렇지만 댓글을 달아주시면 최대한 답변드리고자 노력하겠습니다.
Korean Title : [파이썬] 뷔퐁의 바늘 문제 - 다각형 버전
Buffon's Needle Problem is very popular math problem about 'probability' .
(https://en.wikipedia.org/wiki/Buffon%27s_needle_problem)
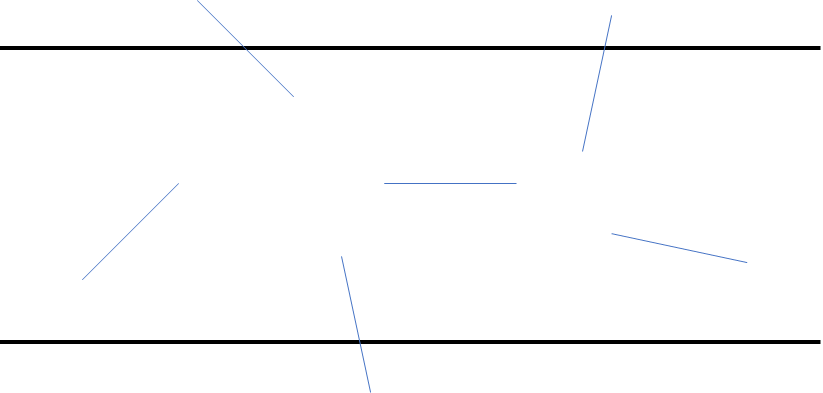
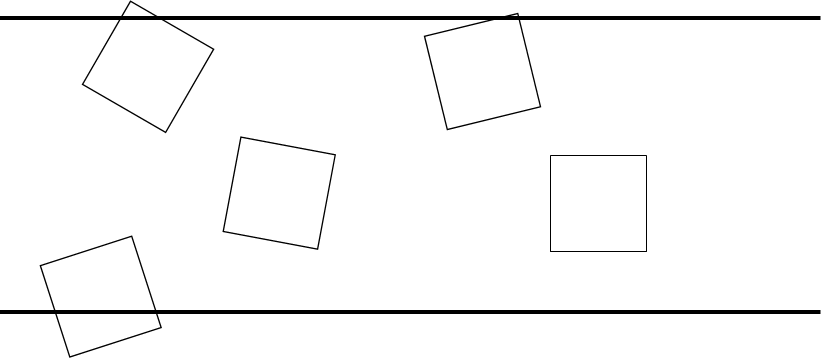
But it can be generalized for the regular polygon case. For example, it can be square instead of needles.
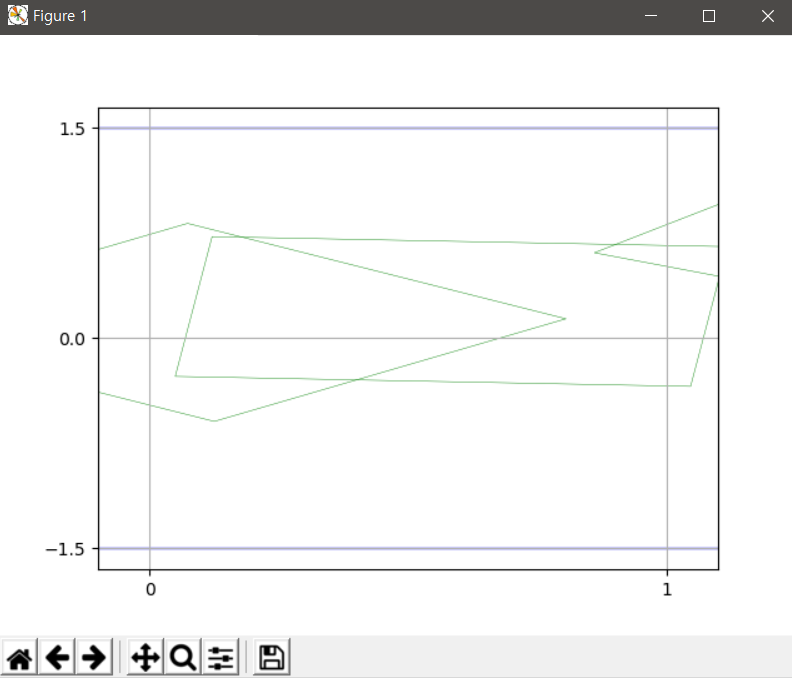
This python code use Monte Carlo method to obtain the probability. And also visualize the result.
""" Made By SturdyCobble
stdcobble.tistory.com """
import math
import random
import numpy as np
from matplotlib.patches import Polygon
from matplotlib.collections import PatchCollection
import matplotlib.pyplot as plt
import matplotlib.ticker as plticker
N = 3
poly=[]
distance=3
width=1
# Information of polygon
polygon=[(0,1),(1,1),(1,0),(0,0)]
cnt=0
patches=[]
for i in range(N):
pol=[]
theta=random.random()*2*math.pi
pnt_x=random.random()*width
pnt_y=random.random()*distance-distance/2
for i in polygon:
# rotation
point=[i[0]*math.cos(theta)-i[1]*math.sin(theta),i[0]*math.sin(theta)+i[1]*math.cos(theta)]
point[0]=point[0]+pnt_x
point[1]=point[1]+pnt_y
pol.append(point)
poly.append(pol)
def is_cross(p1,p2):
if (p1[1]-distance/2)*(p2[1]-distance/2)<0 or (p1[1]+distance/2)*(p2[1]+distance/2)<0:
return True
def counter():
global cnt
for i in poly:
k=i+[i[0]]
for j in range(len(polygon)):
if is_cross(k[j],k[j+1]):
cnt=cnt+1
break
counter()
print(cnt)
print("Probability")
print(cnt/N)
# Visualize the result
for i in poly:
pat=Polygon(i,True, edgecolor='g',facecolor='None',linewidth=0.3)
patches.append(pat)
ax = plt.subplot()
l1=Polygon([(-100000,distance/2),(100000,distance/2)],False,edgecolor='b',facecolor='None')
l2=Polygon([(-100000,-distance/2),(100000,-distance/2)],False,edgecolor='b',facecolor='None')
plt.axis([-width*0.1, width*1.1, -distance*0.55, distance*0.55])
for p in patches:
ax.add_patch(p)
ax.add_patch(l1)
ax.add_patch(l2)
loc1 = plticker.MultipleLocator(base=width)
loc2 = plticker.MultipleLocator(base=distance/2)
ax.xaxis.set_major_locator(loc1)
ax.yaxis.set_major_locator(loc2)
plt.grid(True)
plt.show()
Example :
------------setting---------------
N = 1000
poly=[]
distance=10
width=20
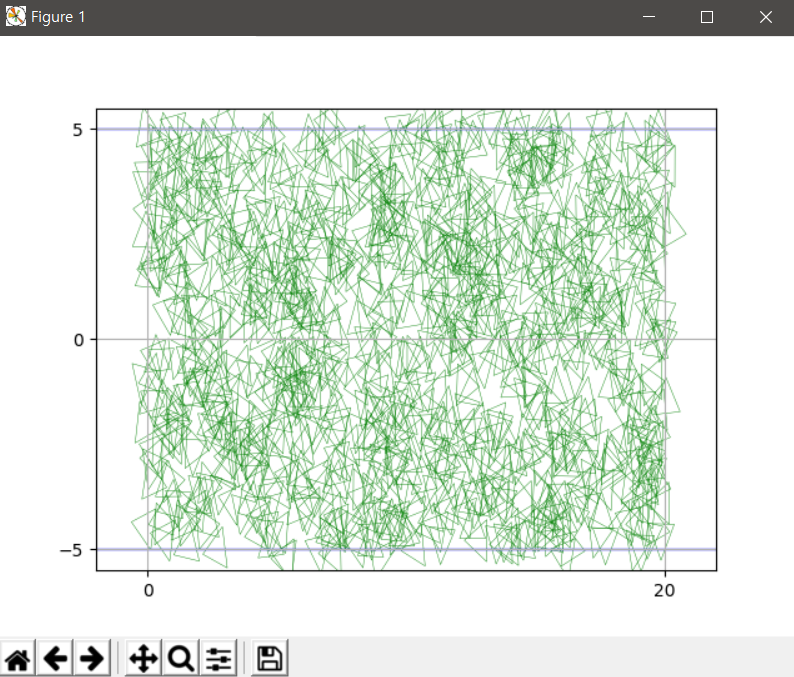
polygon=[(0,1),(1,1),(1,0),(0,0)] # l/d = 0.1
--------------output--------------
133
Probability
0.133
----------------------------------
------------setting---------------
N = 1000
poly=[]
distance=10
width=20
polygon=[(-0.5,0),(0.5,0),(0,math.sqrt(3)/2)]
--------------output--------------
113
Probability
0.113
----------------------------------
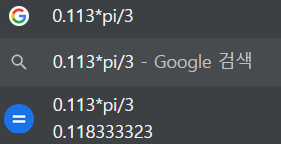
N = 1000
poly=[]
distance=10
width=20
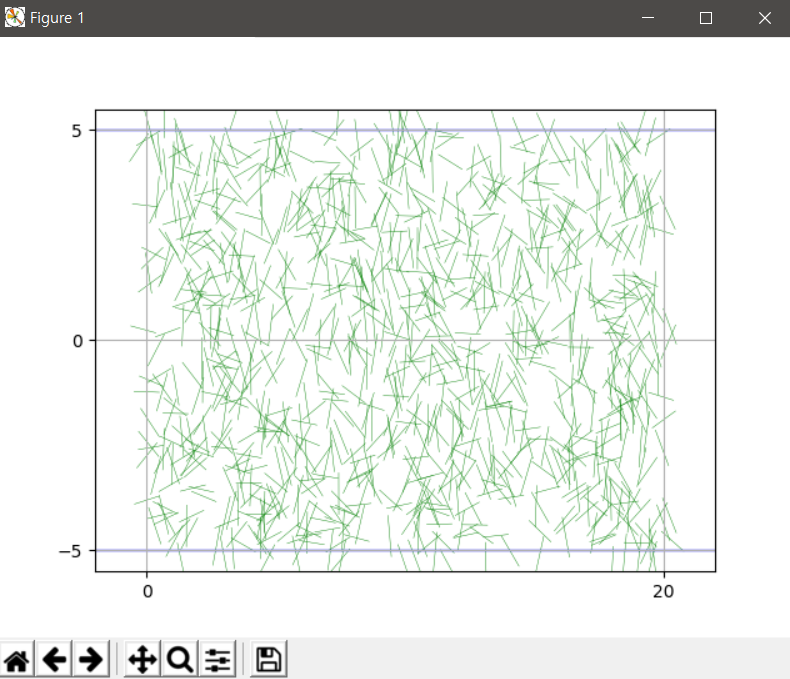
polygon=[(-1,0),(0,0)] # Actually, NOT needle.
-----------output-------------
76
Probability
0.076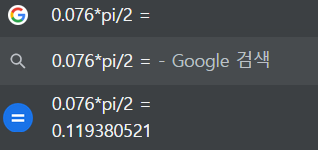
Reference:
https://en.wikipedia.org/wiki/Buffon%27s_needle_problem
Buffon's needle problem - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search The a needle lies across a line, while the b needle does not. In mathematics, Buffon's needle problem is a question first posed in the 18th century by Georges-Louis Leclerc, Comte de B
en.wikipedia.org
https://en.wikipedia.org/wiki/Monte_Carlo_method
Monte Carlo method - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Probabilistic problem-solving algorithm Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain n
en.wikipedia.org
http://gtfe.usal.es/pdfs/ensenanza/santi_int_j_math_edu_sci_irrational_06.pdf
Statistical estimation of some irrational numbers using an extension of Buffon’s needle experiment(S. VELASCO, F. L. ROMAN, A. GONZALEZ, J. A. WHITE, 2005)
